[5]Divide and Conquer
將輸入切分為許多小部分,用遞迴方式解決每一部份再組合起來,得到一個綜合性的答案。很重要的一點是:每一迴圈都會讓問題的大小變小。
Merge Sort Algorithm
將輸入分為兩個大小相同的部分,用遞迴方式解決這兩個子問題,最後組合成一個解法,其中在分割、組合都只花線性的時間。通常用數學歸納法來證明這類演算法的正確性。
在merge sort這一類的演算法中,可以想像在最後一次進入迴圈後,問題被切成最小單位,例如排序兩個數字,那麼就分成兩半,變成各自一個數字(也就代表已經排序好了),就會返回到原先的程序,去做合併的動作。考慮任何符合這類操作的演算法時間複雜度,以T(n)表示worst-case running time,並假設n為偶數。
- Divide:O(n)將輸入分成各自為n/2的大小。
- Conquer:T(n/2),對於每一個切分的部分。
- Combine:O(n)結合兩個遞迴之後的結果。
存在常數C,使得
T(n)≤ 2T(n/2)+cn,當n>2,且T(2)≤ c
Solving Recurrences
兩個基本的作法:
- Unroll直接展開(recursion tree)
- Substituting a guess猜一個答案再用數學歸納法證明(不實用)
Unroll
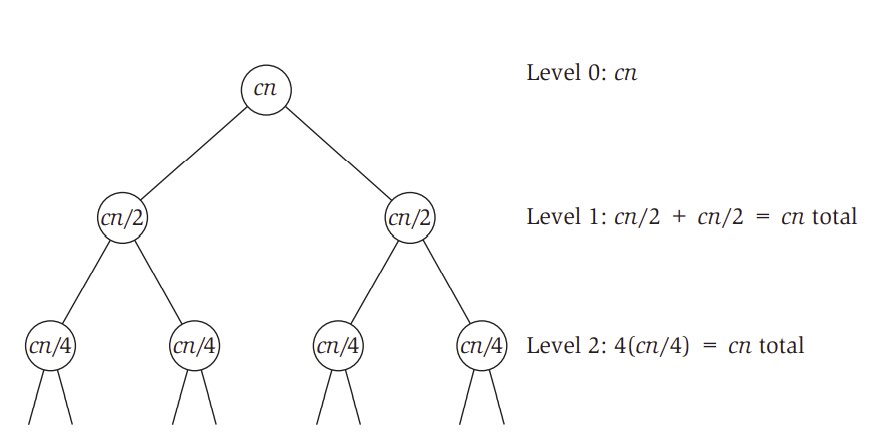
- 展開後,分析前面幾層:在第0層單一問題大小為n,會花最多cn加上遞迴處理子問題的時間;在第二層則是兩個問題大小為n/2,每一問題最多花cn/2+遞迴處理子問題的時間...。
- 辨識確認問題的樣態:(總體來說是怎麼樣?)在第i層時,問題個數變成2^i個,問題大小為n/(2^i),每一問題最多花cn/(2^i),因此,第i層最多花(2^i)*cn/(2^i) = cn的時間。
- 加總遞迴的每一層:我們知道要將問題由n切分到2需要logn(底數為2)次,而每一層又需要花cn的時間,所以總共會是O(cn*logn)=O(nlogn)。
Counting Inversions
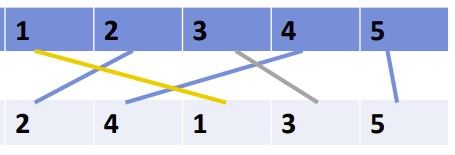
考慮有兩個排序分別為12345及24135,如上圖所示,我們可以看到有三個交叉,稱之為Inversion,發生在(2,1)、(4,1)、(4,3)。這樣檢查Inversion個數可以讓我們比較兩個排序的相似度,實際上就可以應用在像是推薦系統等,透過比較單一使用者和其他資料庫中使用者的喜好順序,找到與其相似的人在進一步推薦相關產品。
另外,若兩排序完全相同稱為complete agreement,inversion個數為0;排序完全相反則稱為complete disagreement,inversion個數為C n取2。
設計演算法
最暴力的方法是去比較每一對,那就是O(n^2)。而最好的解法可以是O(nlogn),稍微改編前面merge sort的作法。
同樣將問題大小n分為兩半,大小為n/2=m,前半為a1~am;後半為am+1~an。我們先分別屬這兩辦當中所含的inversion,接者合併時,會發生的inversion肯定是(ai, aj)其中ai屬於a1~am;aj屬於am+1~an,且ai>aj。
為了數每兩半間的inversion,我們用遞迴方式排序兩半的數字,並在其中計數Inversion數量,這樣會使得在合併的步驟更簡易一些。稱之為Merge-and-Count。
如下圖所示,兩半ab分別都需要有一指標,指到目前合併的註標,合併時,若是b的元素加入merged result,代表有一個inversion發生。
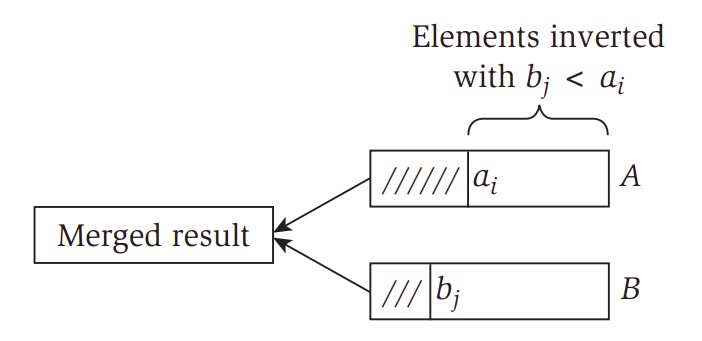
Merge-and-Count
Maintain a Current pointer into each list, initialized to point to the front elements
Maintain a variable Count for the number of inversions, initialized to 0
While both lists are not empty:
Let ai and bj be the elements pointed to by the Current pointer
Append the smaller of these two to the output list
If bj is the smaller one then
Increment Count by the number of elements remaining in A
EndIf
Advance the Current pointer in the list from which the smaller element was selected.
EndWhile
Once one list is empty, append the remainder of the other list to the output
Return Count and the merged list
Sort-and-Count
If the list has one element then
there are no inversions
Else
Divide the list into two halves:
A contains the first ⌈n/2⌉ elements
B contains the remaining⌊n/2⌋ elements
(rA, A) = Sort-and-Count(A)
(rB, B) = Sort-and-Count(B)
(r, L) = Merge-and-Count(A,B)
Endif
Return r = rA+rB+r, and the sorted list L
Merge-and-Count為O(n),而整個需要Sort-and-Count的時間複雜度T(n)也滿足前面提到的切分、計算合併的程序,因此n個元素的時間複雜度為O(nlogn)。
Closest Pair of Points
問題
給定一二維座標中含有n點,找到距離最近的一對。
設計演算法
用最暴力的解法當然還是兩兩相比,時間複雜度維O(n^2)。但我們可以改善成O(nlogn),甚至在更進階一些利用randomization可以到O(n)(這裡不討論)。
符號定義與假設
- 點集合P = {p1,...,pn},其中pi有座標 (xi,yi),在任一兩點pi,pj間用(pi, pj)表示兩點間的歐式距離
- 沒有兩點有相同的x、y座標。(這一點非必要,也有方法消除,但為了簡化先做此假設)
想法
我們同樣用divide&conquer的想法,在左半邊找到有最短距離的pair;右半邊也找到有最短距離的pair,最後在linear時間內用這些資訊找到解答。如果可以發展這樣的作法,就可將時間限縮在O(nlogn)。
這樣的想法最大的難處在於:我們在合併時還需要考慮那些界在左右半邊之間的pair是否才是擁有最短距離的,最差的情況還是要Ω(n^2)才做得到,然而為了追求好的效率,應想辦法在O(n)的時間內辦到。
視覺化
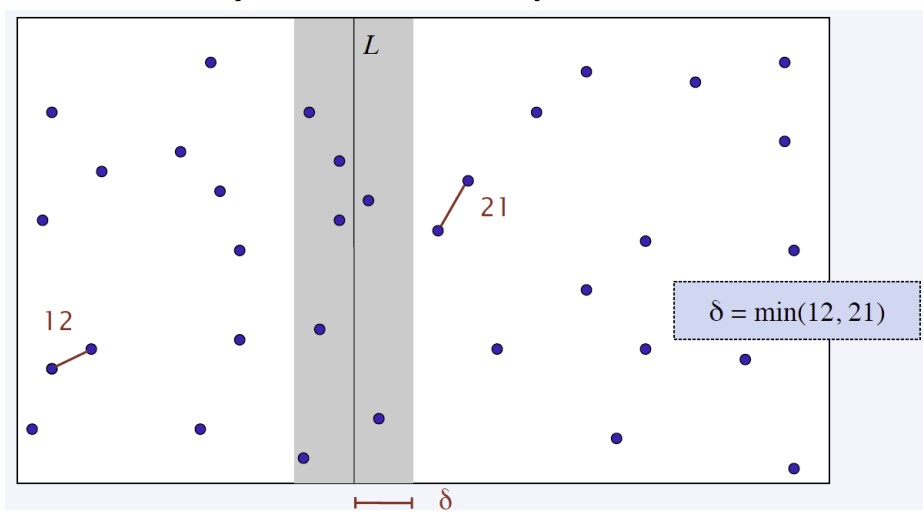
Divide:先以x座標排序個點,並切分成兩部分
Conquer:找到各自的最小距離pair
Combine:最多只需要找距離中線L左右δ內的點就行,其中δ = min(左邊最近pair距離, 右邊最近pair距離)
Combine
對點以y座標軸做排序

只要檢查7個點
若|j-i|>7,那麼Si, Sj的距離至少已經是δ
證明
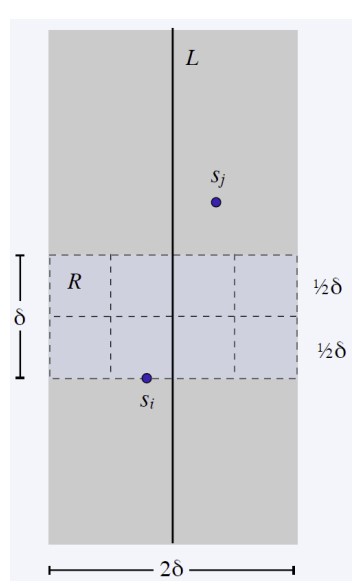
查看下圖,有一長寬為δ、2δ的長方形,將其切分為8格。
- 所有超過格子的點和si距離超過δ。
- 同一格內最遠距離為對角線,長度為(√2/2)*δ,小於δ,那早就該被找到。
Algorithm
Closet-Pair(p1,...,pn)
Compute vertical line L splitting the plane evenly [O(n)]
δ1 = Closet-Pair(points in the left side)
δ2 = Closet-Pair(points in the right side)
δ = min{δ1, δ2}
Delete all points further than δ from line L [O(n)]
Sort remaining points by y-coordinate [O(nlogn)]
Scan points in y-order and compare distance between each point and next 7 neighbors [O(n)]
If any of these distances is less than δ, update δ
Return δ
時間複雜度:T(n) =T⌊n/2⌋+T⌈n/2⌉ + nlogn。瓶頸在於排序,我們不想要每次都從頭開始排序點。
讓每次遞迴都回傳兩lists:所有點依x座標排序、所有點依y座標排序。接著用合併兩個以排序的lists去排序。
NEED TO UPDATE
Closet-Pair(p1,...,pn)
Compute vertical line L splitting the plane evenly [O(n)]
δ1 = Closet-Pair(points in the left side)
δ2 = Closet-Pair(points in the right side)
δ = min{δ1, δ2}
Delete all points further than δ from line L [O(n)]
Sort remaining points by y-coordinate [O(nlogn)]
Scan points in y-order and compare distance between each point and next 7 neighbors [O(n)]
If any of these distances is less than δ, update δ
Return δ